Untying the secret of Celtic knots

‌

Benjamin Liu

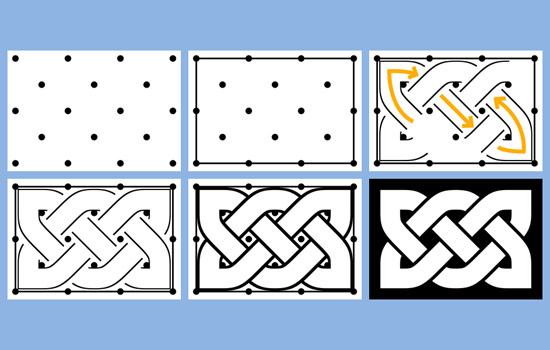
Drawing a Celtic knot on a grid.

The hypnotic Celtic knot might not be as complicated as it seems.

Fourth-year math major Benjamin Liu, from Northampton, Mass., has broken the Celtic knot into 12 standard segments that can be rearranged to create variations of the interlacing, decorative strands. He wrote a computer program to produce the knots faster than he could by hand, though it was “tricky,” he says, to program the curves and to create overlapping strands.

Liu will share his computer-generated knot work with visitors to his exhibit, Exploring Celtic Knots, located on the first floor of Institute Hall during the Imagine RIT: Innovation and Creativity Festival this Saturday, May 4. Festivalgoers will be able to manipulate user-friendly computer programs of Celtic knots and arrange actual patterned tiles. Liu designed his exhibit to appeal to a wide audience.

Liu’s interest in knot patterns began with a YouTube video that showed how to draw knots on grid paper.

“What struck me was how complex the patterns could be, yet how relatively simple the process was,” Liu says. “You start with a sort of schematic diagram that the knot will follow, and the knot simply arises when the correct rules for coloring in the diagram are followed. This lends itself quite well to programming.”

He quickly realized he could tie a knot “one tile at a time.”

“Then, you could break the tiles apart and, with just a few standard tiles (12 or so), you could create any Celtic knot,” Liu says. “If you had these 12 types of tiles you could make a mosaic of any knot you wanted.”

In addition to Liu, exhibitors also include Matthew Hoffman, professor in the School for Mathematical Sciences, who helped construct the tile trays; Melissa Ziankoski, a graduating senior majoring in philosophy; and Valerie Altounian, a graduating senior from the medical illustration program.

Liu’s fellow exhibitors support his interest in his efforts to understand and replicate Celtic knots. They will assist visitors to the exhibit and explain aspects of the patterns.

“Mathematically it’s interesting that the many Celtic knots you can generate in this way all have the same type of underlying structure,” Liu says. “The designs can seem very complicated but the schematics are not. This concept is very familiar to mathematicians and computer scientists.”