Ph.D. student uses computing to help solve 90-year-old math problem
David Narváez was part of multi-university research team that settled Keller’s conjecture
Marijn Heule
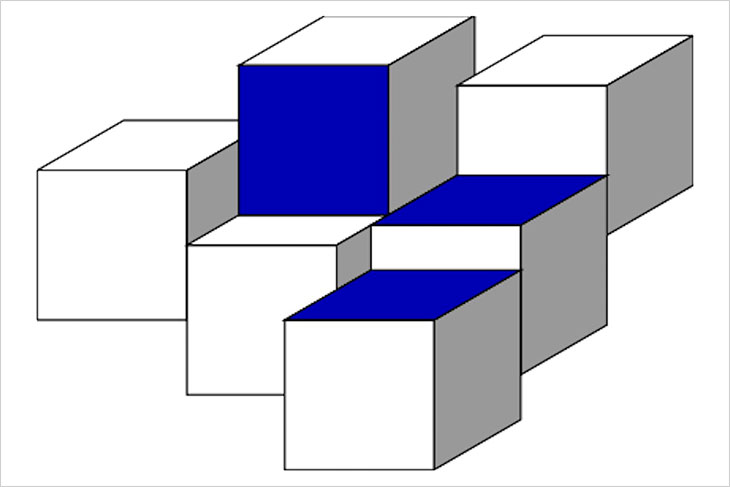
An RIT student used mathematical computing to help researchers solve a nearly century-old math problem called Keller’s conjecture. This image depicts Keller’s conjecture in a three-dimensional space, where tiling the entire space with identical cubes would result in at least one pair of cubes meeting face-to-face.
A Rochester Institute of Technology Ph.D. student was part of a team of researchers that settled a 90-year-old math problem called Keller’s conjecture.
David Narváez, a computing and information sciences Ph.D. student, who helped resolve Keller’s conjecture
David Narváez, a computing and information sciences Ph.D. student, used his expertise in symmetry-breaking to help a cluster of computers solve the problem in just 30 minutes. He also brought in techniques that make the proof verifiable, meaning that mathematical computer programs can confirm the answer is correct.
“I enjoy using computer science to help solve problems that mathematicians are stuck with,” said Narváez, who is from Panama.
Keller’s conjecture is a tiling problem about how certain shapes can cover a space. It was posed by Ott-Heinrich Keller in 1930.
The conjecture asserts that if you cover an n-dimensional space with n-dimensional identical hypercubes, at least two of the hypercubes must share a face. For example, if you’re trying to completely cover a cube with matching square bricks, there should always be at least one pair of bricks that meet exactly face-to-face. The conjecture makes the same prediction for spaces of every dimension.
Throughout the past 90 years, mathematicians have explored the conjecture. It was proven true for dimensions one through six. It was then proven false in eight dimensions and higher. The last mystery was if the conjecture was true in seventh-dimensional spaces.
In fall 2019, Narváez joined Joshua Brakensiek of Stanford University and Marijn Heule and John Mackey of Carnegie Mellon University to put the unresolved question to bed. Narváez, who enjoys solving combinatorial problems using constraint satisfaction techniques, was invited to help solve the problem after collaborating with the researchers on a previous project. The team recently published a paper on their work.
The team was using an automated reasoning approach that would allow high-powered computers to systematically check all possibilities to see if Keller’s conjecture was true for seventh-dimensional spaces. However, the researchers said that it would take the world’s fastest computers until the end of time before they’d exhausted all the possibilities.
“The problem with these kinds of mathematical objects is they’re highly structured, with many similarities,” said Narváez. “There are a lot of calculations that can be avoided if you take into account those symmetries. But the computer logic doesn’t know that, so it repeats a lot of work.”
Narváez essentially taught the computer about what symmetries could be avoided, helping to discard big chunks of the problem and save time.
“Without symmetry breaking, the automated approach is unable to solve the conjecture,” said Heule, who is an associate professor at Carnegie Mellon. “Implementing symmetry breaking is hard and we had to be sure that no mistakes were made.”
An important part of Narváez’s symmetry-breaking argument is that his technique also turned it into a machine-checkable proof, giving the researchers confidence in the correctness of the implementation. The technique produced an enormous proof of roughly 200 gigabytes. However, the answer that comes out of the computer is often too complicated to be understood by human beings, so it needs to be verifiable by a mathematical computer program.
“Resolving Keller’s conjecture shows that automated reasoning is able to solve mathematical challenges that have been open for decades,” said Heule. “It is important to have technologies that can solve problems that are too hard for humans. The same techniques are used to show the correctness of highly complex systems, which are everywhere, from finance to health care to aviation.”
After graduating, Narváez plans to continue solving math problems as a computer science postdoctoral researcher at University of Rochester in the spring. He was selected for the 2020 class of Computing Innovation Fellows.
To learn more about the resolution of Keller’s conjecture, go to Heule’s website.